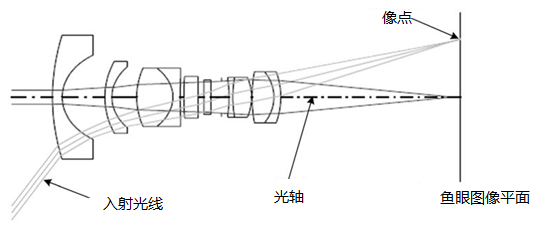
鱼眼模型介绍

这里直接截取鱼眼镜头的成像原理到畸变矫正的原文作为此文的引子：

鱼眼镜头一般是由十几个不同的透镜组合而成的。在成像的过程中，入射光线经过不同程度的折射，投影到尺寸有限的成像平面上，使得鱼眼镜头与普通镜头相比起来拥有了更大的视野范围。

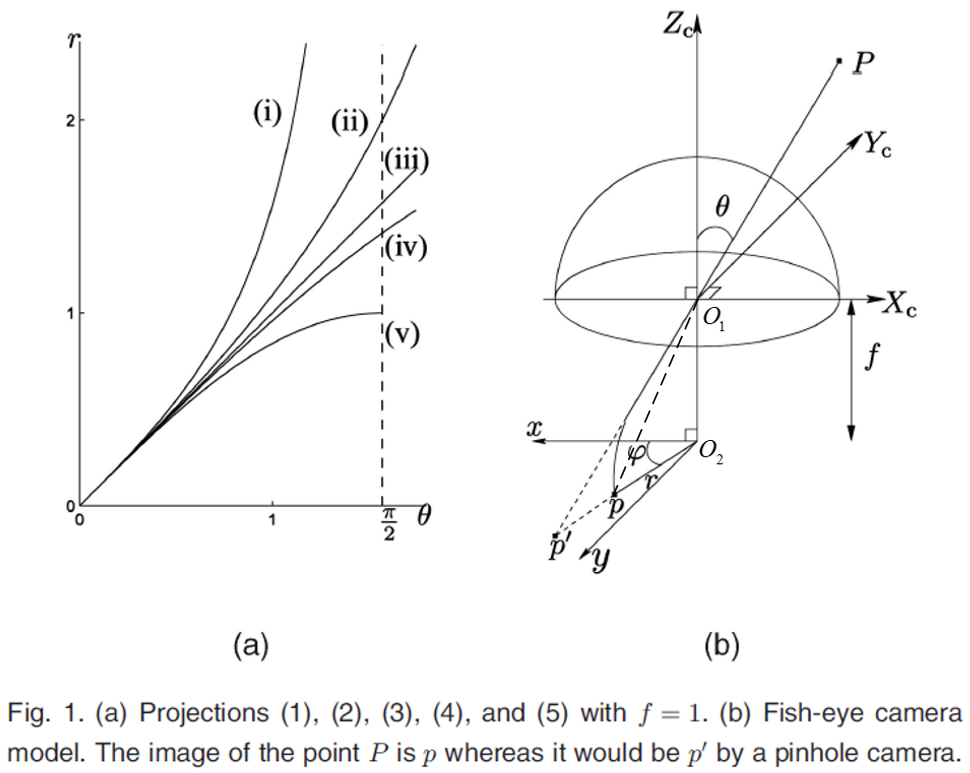
在研究鱼眼相机成像时，可以将上面的镜头组简化为一个球面：

图中，$O_1-X_cY_cZ_c$是相机坐标系，$O_2-xy$是成像平面。世界中有一点$P$，入射角为$\theta$。如果按照针孔相机模型，入射光线$PO_1$经过镜头后不改变路线，$p’$为$P$的成像点。但对于鱼眼相机，入射光线经过镜头后会发生折射，因此$p$才是$P$的成像点，极坐标表示为$(r, \varphi)$ 。

可以用投影函数来对光线的折射建模。根据投影函数的不同，鱼眼相机的传统模型大致能被分为五种：透视投影（即针孔相机模型）、等积投影、等距投影、体视投影、正交投影。

投影模型投影函数特征
i. 透视投影 (perspective projection)$r = ftan\theta$针孔相机模型
ii. 体视投影 (stereographic projection)$r = 2ftan\frac \theta 2$​任何直线相交的角度，在变换后保持不变
iii. 等距投影 (equidistance projection)$r = f\theta$物体成像面上距离画面中心的距离与入射角成正比
iv. 等积投影 (equisolid angle projection)$r = 2fsin\frac \theta 2$​在变换前后，物体所占的立体角大小不变
v. 正交投影 (orthogonal projection)$r = fsin\theta$投影畸变最大，而且最大视场角不能大于180°

OpenCV所用模型

先看OpenCV文档的原文：

Let $P$ be a point in 3D of coordinates X in the world reference frame (stored in the matrix X) The coordinate vector of $P$ in the camera reference frame is:

$Xc = R X + T$

where $R$ is the rotation matrix corresponding to the rotation vector om: $R$ = rodrigues(om); call x, y and z the 3 coordinates of $Xc$:

$x=Xc_1$

$y=Xc_2$

$z=Xc_3$

The pinhole projection coordinates of P is $[a; b]$ where

$a=x/z$

$b=y/z$

$r^2=a^2+b^2$

$θ=arctan(r)$

Fisheye distortion:

$θ_d=θ(1+k_1θ^2+k_2θ^4+k_3θ^6+k_4θ^8)$

The distorted point coordinates are $[x’; y’]$ where

$x′=(θ_d/r)a$

$y′=(θ_d/r)b$

Finally, conversion into pixel coordinates: The final pixel coordinates vector $[u; v]$ where:

$u = f_x (x’ + \alpha y’) + c_x$

$v = f_y y’ + c_y$

查看cv2::fisheye::initUndistortRectifyMap的实现，和文档描述的一致：

void cv::fisheye::initUndistortRectifyMap( InputArray K, InputArray D, InputArray R, InputArray P,
    const cv::Size& size, int m1type, OutputArray map1, OutputArray map2 )
{
    // ...
    for( int i = 0; i < size.height; ++i)
    {
        // ...
        for( int j = 0; j < size.width; ++j)
        {
            double u, v;
            if( _w <= 0)
            {
                u = (_x > 0) ? -std::numeric_limits<double>::infinity() : std::numeric_limits<double>::infinity();
                v = (_y > 0) ? -std::numeric_limits<double>::infinity() : std::numeric_limits<double>::infinity();
            }
            else
            {
                double x = _x/_w, y = _y/_w;

                double r = sqrt(x*x + y*y);
                double theta = atan(r);

                double theta2 = theta*theta, theta4 = theta2*theta2, theta6 = theta4*theta2, theta8 = theta4*theta4;
                double theta_d = theta * (1 + k[0]*theta2 + k[1]*theta4 + k[2]*theta6 + k[3]*theta8);

                double scale = (r == 0) ? 1.0 : theta_d / r;
                u = f[0]*x*scale + c[0];
                v = f[1]*y*scale + c[1];
            }
			// ...
        }
    }
}

探讨

现在问题来了，

$\theta=arctan(r)$是怎么来的？

实际是$\theta = arctan(r/f)$。由于建模时用的是归一化的球面和像平面，故$f$为1

$u = f_x (x’ + \alpha y’) + c_x$里的$\alpha$是什么？

$\alpha$为skew coefficient。“skew"指成像平面x轴和y轴的角度。理想的成像平面x轴和y轴是垂直的，但现实中x轴和y轴可能是倾斜的，进而产生倾斜的图片。为了纠正此偏差，需要对图片施加一个仿射变化。由于大部分厂商的CCD是直角的，故用OpenCV标定时会使用CALIB_FIX_SKEW的flag，$\alpha$设为0

$θ_d=θ(1+k_1θ^2+k_2θ^4+k_3θ^6+k_4θ^8)$是怎么来的？

按照论文《A Generic Camera Model and Calibration Method for Conventional, Wide-Angle, and Fish-Eye Lenses》，为了方便鱼眼相机的标定，一般取$r$关于$\theta$泰勒展开式的前5项来近似鱼眼镜头的实际投影函数，即

$r_d \approx θ(1+k_1θ^2+k_2θ^4+k_3θ^6+k_4θ^8)$

那么，这里为什么是$\theta_d$而非$r_d$？

解释一

鱼眼镜头的成像原理到畸变矫正一文给出下图，并作解释

由几何关系有

$r_d = f * tan(\theta_d) = tan(\theta_d)$

考虑到相机的成像CCD平面尺寸一般都是几毫米，焦距在几百毫米左右，所以相机实际成像过程中$\theta_d$通常很小，此时$tan(\theta_d) \approx \theta_d$，故有

$r_d = tan(\theta_d) = \theta_d = θ(1+k_1θ^2+k_2θ^4+k_3θ^6+k_4θ^8)$

问题是，推导模型时用的是归一化的球面和成像平面，$\theta_d$并不总是很小。比如，当$(x’,y’)=(1,1)$时，$r_d=\sqrt2$，$\theta_d=arctan(r_d)\approx0.955$，此时将$\theta_d$近似为$tan(\theta_d)$并不合理。

解释二

鱼眼投影模型理解以及opencv官方文档和同类文章勘误 - 知乎给出的解释则是，

OpenCV文档里的$\theta_d$并不是折射角，对应的实际是图中的$r_d$，这只是一个误导性的变量名称。

解释三

结合Stack Overflow的讨论，我的解释是，$\theta_d$指的就是用多项式修正后的入射角，而非折射角，也不是成像点在像平面上的极坐标半径（尽管后面会看到它们数值相等）。OpenCV对鱼眼成像的建模过程如下：

  1. 对于世界坐标系中任一点$P$，计算其在针孔相机坐标系中的投影坐标$[a, b]$，再计算出该点在相机坐标系极坐标半径$r$和入射角$\theta$
  2. 实际很少有perfect angular fisheye lenses，镜头会有一定非线性的存在。考虑到这一点，将入射角修正为$\theta_d = \theta (1 + k_1 \theta^2 + k_2 \theta^4 + k_3 \theta^6 + k_4 \theta^8)$
  3. 采用等距投影模型（$r=f\theta_d$），将相机坐标系的点投影到图像平面。有$x’=(\theta_d/r)a$, $y’=(\theta_d/r)b$
  4. 在归一化球面和像平面上，$f=1$，故同样有$r=\theta_d=\theta (1 + k_1 \theta^2 + k_2 \theta^4 + k_3 \theta^6 + k_4 \theta^8)$

从结果上看，此种解释和解释二是等效的。

事实上，无论是像此种解释一样将投影、畸变分开处理，还是像解释二一样将整个过程用一个多项式拟合，都是可行的。

记投影函数为$P(\theta)$，多项式畸变函数为$D(\theta)$，如果将投影-畸变视为独立的过程，那过程函数是$r=P(D(\theta))$，而$P(D(\theta))$完全可以用另一个多项式$E(\theta)$拟合，即$r=P(D(\theta))=E(\theta)$。$D$和$E$都是多项式函数，只不过其系数随$P$的具体形式可能完全相同（等距投影），也有可能不同（其它非线性投影）。

至于鱼眼镜头的成像原理到畸变矫正给出的图，

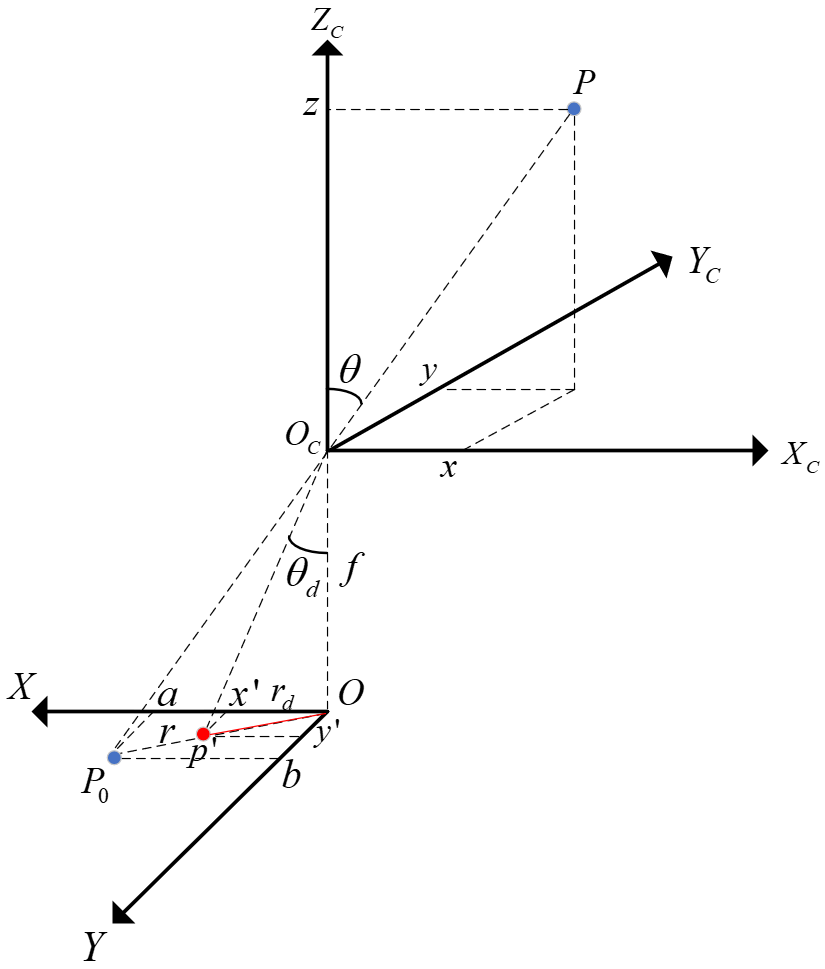
如果对照此图，很容易认为$\theta_d$是折射角而非入射角，且可以进而推出$r_d=ftan\theta_d$，这岂不是与上面用的等距投影$r=f\theta_d$矛盾？

我的看法是，这张图与OpenCV的投影模型无关，如果硬按照此图理解OpenCV的鱼眼模型，当然是会产生矛盾的。OpenCV文档本身没有给出示意图，按个人理解，其过程及所用符号的含义更接近论文的原图，这里我额外标记了$\theta_d$：

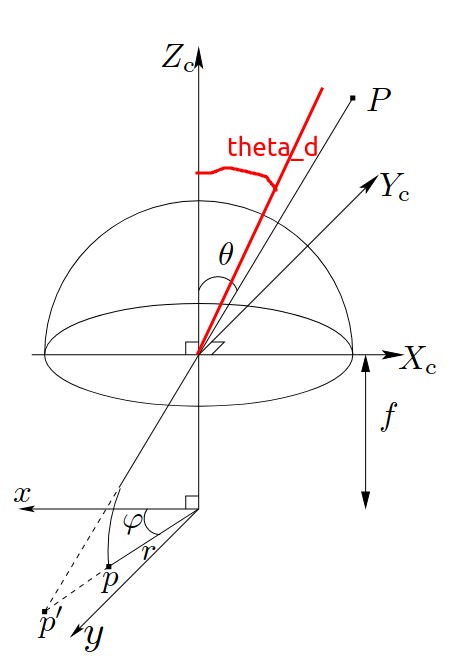
由于$\theta_d$并非折射角，所以$r_d=ftan\theta_d$自然也是不成立的。

当FOV>180°时，此模型还成立吗？

从OpenCV Fisheye Calibration FOV 220 - Python - OpenCV及Calibrating fisheye lenses above 180 degrees - OpenCV Q&A Forum的讨论来看，OpenCV当前是不支持超过180°FOV鱼眼的标定的

总结

综上，我理解OpenCV的鱼眼模型其实是等距投影模型+多项式畸变模型。

参考